../spectral-bias

Published on: 2025-05-21

Why Frequency Matters in Neural Networks - "On the Spectral Bias of Neural Networks" [ICML 2019]

About Author

Nasim Rahaman pursued his PhD jointly at the Max Planck Institute for Intelligent Systems (MPI-IS) in Tübingen, Germany, and Mila – Quebec AI Institute in Montreal, Canada.

At MPI-IS: He was part of the Empirical Inference Group, supervised by Bernhard Schölkopf.
At Mila: He was co-supervised by Yoshua Bengio.

Abstract

Neural Networks are a class of highly expressive functions that are able to fit even random input-output mapping with 100% accuracy.

By using Fourier Analysis, they showed network learning bias towards low-frequency functions, termed as "Spectral Bias", this property aligns the observation that over-parameterized networks prioritize learning simple patterns that generalize across data samples.

This is a very mathmatical paper, if you are interested in seeing proof or demostration in detail, please check back to original paper.
I will briefly mention math parts in a more abstract view.

2. Fourier Analysis of ReLU Networks

They call "ReLU Network" a scalar function $f: \mathbb{R}^d \rightarrow \mathbb{R}$, which takes a series of input data $x$ into a regression value $y$.

ReLU networks are known to be continuous piece-wise linear (CPWL) functions¹, in reverse, every CPWL function can be represented by a ReLU network.

So we can make the piecewise linearity explicit by writing:

$$f(x) = \sum_{\phi} 1_{P_\phi}(x) (W_\phi x + b_\phi)$$

where $\phi$ is a neuron and $1_{P_\phi}$ is dead neuron indicator.

They further provide:

Lemma 1: how ReLU network can be decomposed by Fourier transform.
Lemma 2: the decay rate of the Fourier transform is direction-dependent, influenced by the structure of the polytopes².
Theorem 1: network overall spectral decay rate differs by directions, mostly $\frac{1}{||k||^{-(d+1)}}$ with occasitional $\frac{1}{||k||^{-2}}$ in orthogonal direction.

So ReLU network has anisotropic spectrum and is weak on high-frequency response. Even without considering training process, ReLU naturally prefers low-frequency once initialized.

During training phase, gradiant majorly tuned by higher amplitute components in spectrum which are low-frequencies, both structure itself and training process focus on higher dynamics at begining.

Footnotes:

The whole function is continuous but divided in many areas, each area is linear inside itself, its ability is expressed by how dense the division are.

The cluttered areas compose as a polytope in a high-dimension space. (Imagine multi-faces approximated ball object in 3D space)

3. Lower Frequencies are Learned First

To answer questions:

Do NNs really learn lower frequencies first then higher ones during training?
Is "Spectral Bias" a general phenomenon?
Does any of Sturcture, Optimizer, Training data and Objective Funtion has influence on this trend?

They designed 4 experiments:

Sine wave decomposition
Adding perturbation on random parameters on converged model
Adding noise into MNIST dataset
High-dimensional manifold fitting different functions

Experiment 1

They set a 1D Sine wave function:

$$f(x) = \sum_{i} A_{i} \sin(2 \pi k_i x + \phi_i)$$

and use a fully-connected ReLU network to fit it, then display normalized magnitudes of each frequency as following figure 1:

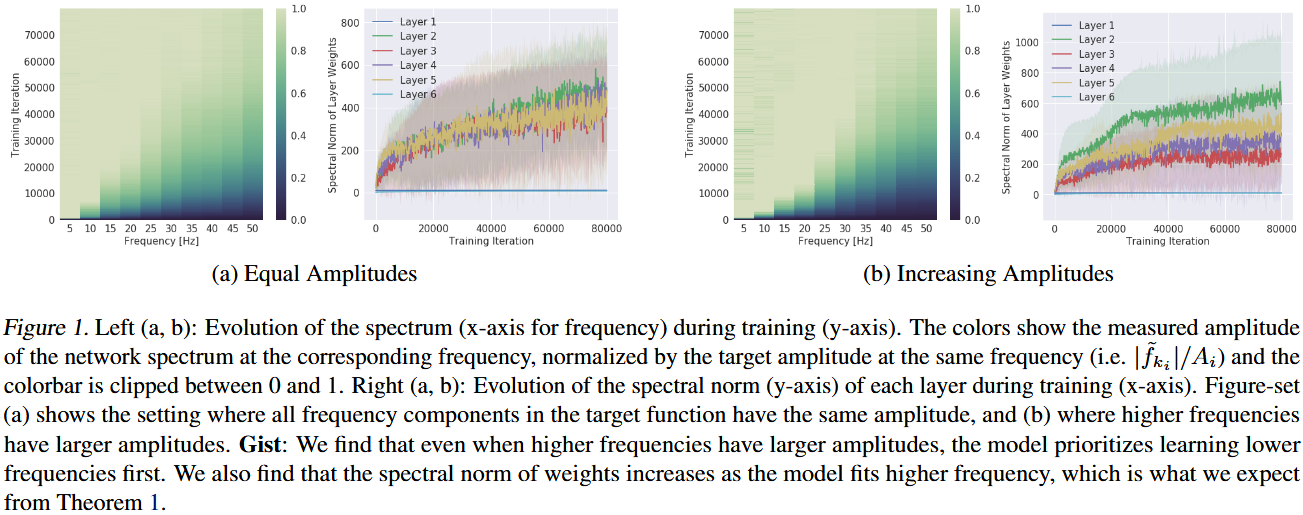
No matter on equal amplitude or increasing with frequency, network all showed clearly low-frequency learning tendency.

This can also be viewed in following figure 2 on how gradually network learns curve:

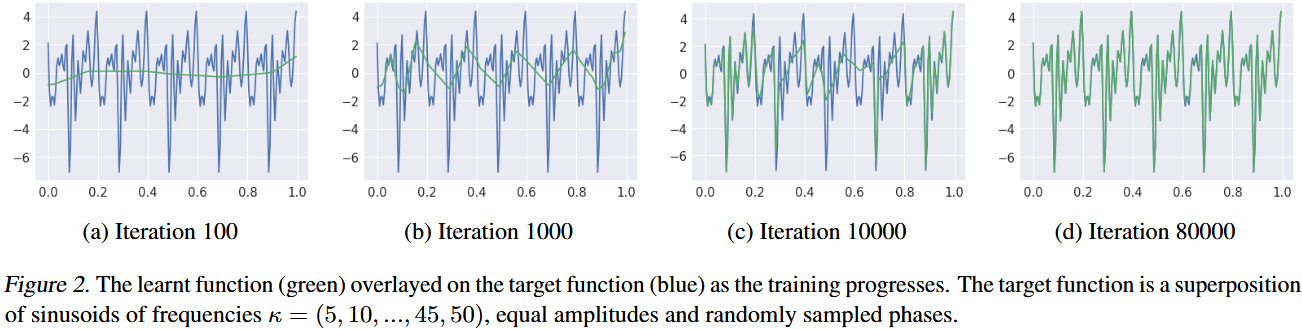
Experiment 2

Follows the experiment 1, they add random noises to converged parameters and see their influences on different frequencies as figure 3:

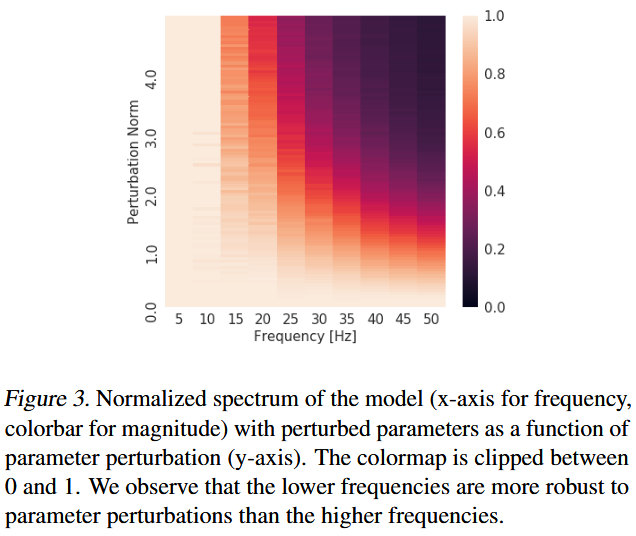
where network shows great robustness on lower freqencies than higher ones.

Experiment 3

They tested 4 different scenarios:

low-freq with different amplitudes
high-freq with different amplitudes
low amplitudes with different freq
high amplitudes with different freq

The results are shown as following figure 4:

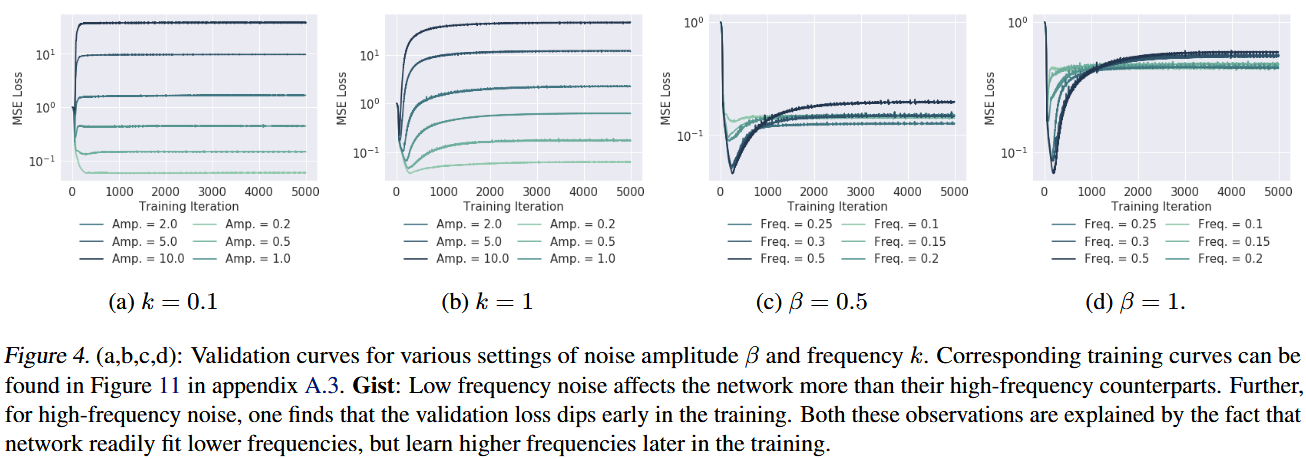
When applying low-freq noises, it almost immediatedly affect the validation results, but applying high-freq noises the loss will drop first then back to similar scalar point as adding low-freq noises.

This actually shows us model is learning lower frequencies at begining and will try to fit high parts gradually.

Part c and d just further proved that by showing different dip depth of loss by lower vs. higher frequency noises.

Experiment 4

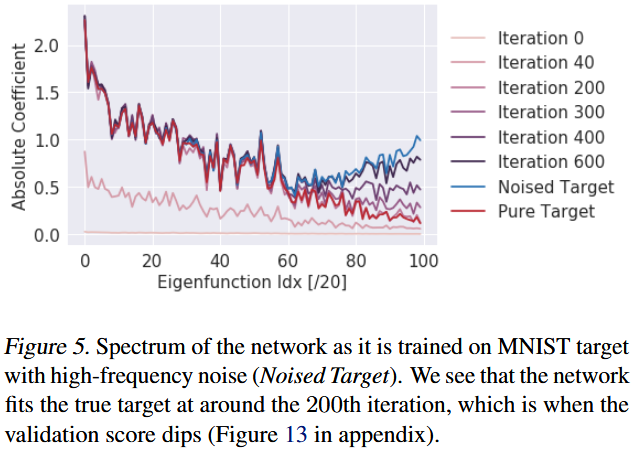
4. Not all Manifolds are Learned Equal

Question: How Spectral Bias changes when the data lies on a lower dimensional manifold³ embedded in the higher dimensional input space of the model.

If we define a mapping: $\gamma: z \in [0,1] \rightarrow x \in \mathbb{R}^2$ such as $\gamma(z) = (z, z^2)$, and a target function: $\lambda(z) = \sin(2 \pi k z)$.

So imagine the target function for network to fit becomes:

$$f(x) = \lambda(\gamma^{-1}(x)) = \sin(2 \pi k z), with \space x = \gamma(z)$$

which means high-frequency occurs on space $z$ but it performs like low-frequency after projecting on input space $x$.

As they sample points from the curve by 2D coordinates on space $x \in \mathbb{R}^2$, to see if network can fitting target $\lambda(z)$.

They did 2 experiments on this problem and got following figure 6, 7 and 8:

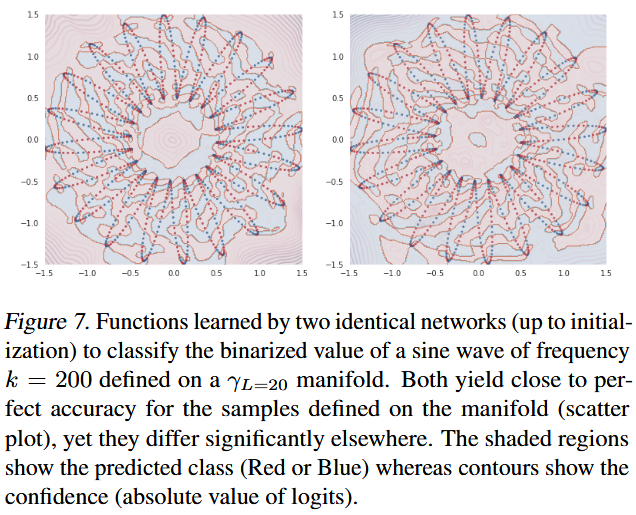
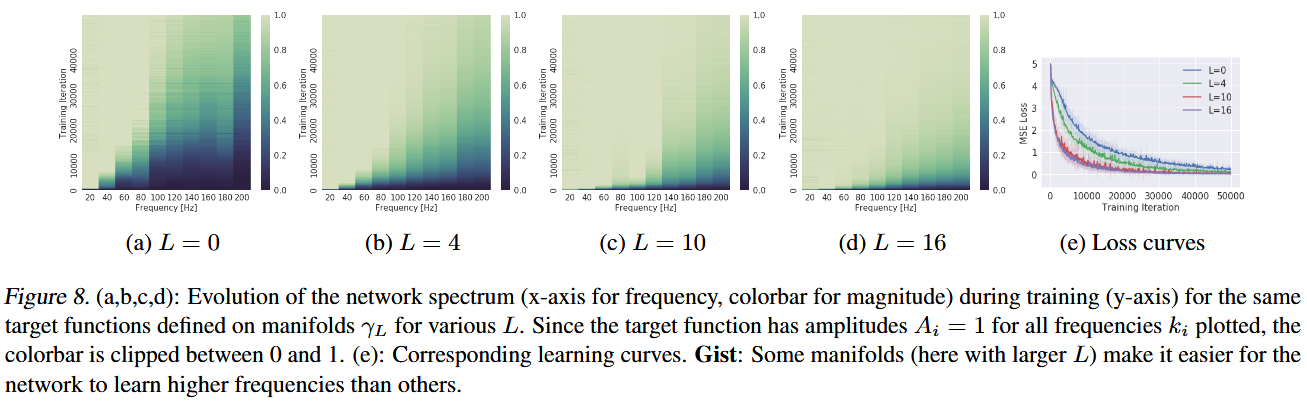
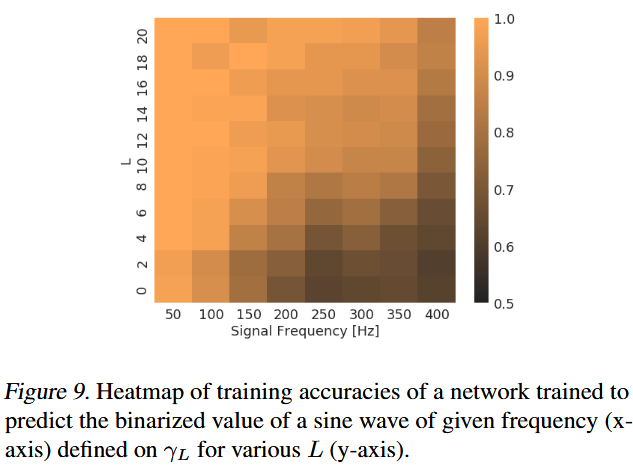
That shows several key points:

If we embed a high-frequency function into high-dimension space, it could behavors more like "low-frequency".
In input space, function is not oscillating strongly, from that space, it becomes more "smooth".
Since "Spectral Bias", network learns better on that low-frequency inputs.

What do those points tell us?

Frequency is relative defined on relative path rather coordinate system.
A high-frequency manifold in low-dimension space could be low-frequency in high-dimension space.
Frequency can be compressed or stretched by embedding mapping.
Imagine $\frac{d}{dz} f(\lambda(z)) = \triangledown_{x} f(x) \cdot \frac{d \lambda}{dz}$, if $\gamma(z)$ changes fast (equal to $\frac{d \lambda}{dz}$ changes fast), $\triangledown_{x} f(x)$ will need to be less fast / become low-frequency.
Generalization ability will be affected by manifold.
If we constraint training data on some low-dimension manifold, network will easier to capture patterns and thus brings training efficiency and generalization ability.

Imagine drawing a curvy line (like sine wave) using your hand by a pen, if the pen shakes given your hand position $z$ fast, even your hand are moving in low-freqency mode, the final line you draw would be a very high-frequency function.